Chapitre 5 Une piste pour protéger des données : la cryptographie

La cryptographie est la branche des mathématiques qui s’occupe spécifiquement de protéger des messages. Jusqu’en 1999, l’usage de techniques cryptographiques était interdit au grand public. C’est devenu légal entre autres pour permettre aux services marchands sur Internet de se faire payer sans que les clientes se fassent piquer leur numéro de carte bancaire.

La cryptanalyse est le domaine consistant à « casser » les techniques cryptographiques, par exemple pour permettre de retrouver un message qui avait été protégé¹⁰⁶.

Lorsque l’on veut protéger des messages, on distingue trois aspects :

confidentialité : empêcher les regards indiscrets ;
authenticité : s’assurer de la source du message ;
intégrité : s’assurer que le message n’a pas subi de modifications.

On peut désirer ces trois choses en même temps, mais on peut aussi vouloir seulement l’une ou l’autre. Une personne écrivant un message confidentiel peut souhaiter nier en être l’autrice (et donc qu’on ne puisse pas l’authentifier). On peut aussi imaginer vouloir certifier la provenance (l’authenticité) et l’intégrité d’un communiqué officiel qui sera diffusé publiquement (donc loin d’être confidentiel).

Dans tout ce qui suit, on va parler de messages, mais les techniques cryptographiques s’appliquent de fait à n’importe quels nombres, donc à n’importe quelles données, une fois numérisées.

À noter, la cryptographie ne cherche pas à cacher les messages, mais à les protéger. Pour cacher des messages, il est nécessaire d’avoir recours à des techniques stéganographiques (comme celles utilisées par les imprimantes évoquées auparavant, ou encore au chiffrement répudiable), que nous ne développerons pas ici.

5.1 Protéger des données des regards indiscrets

Le chiffrement est la piste la plus sérieuse pour que des données ne puissent être comprises que par les personnes « dans le secret ». Les enfants qui utilisent des codes pour s’échanger des mots ou les militaires qui communiquent leurs ordres l’ont d’ailleurs très bien compris !

Le chiffrement d’un fichier ou d’un support de stockage permet de le rendre illisible pour toute personne qui n’a pas le code d’accès (souvent une phrase de passe). Il sera certes toujours possible d’accéder au contenu, mais les données ressembleront à une série de nombres aléatoires, et seront donc incompréhensibles et inutilisables.

Souvent on dit crypter et décrypter à la place de chiffrer et déchiffrer, ce qui peut prêter à confusion. On préfèrera cependant éviter l’emploi de l’anglicisme crypter, et réserver décrypter à l’opération consistant à déjouer un système de chiffrement (c’est-à-dire consistant à « déchiffrer » un message sans connaître le code secret de chiffrement).

5.1.1 Comment ça marche ?

Grosso modo, il y a seulement trois grandes idées pour comprendre comment on peut chiffrer des messages¹⁰⁷.

La première idée : la confusion. Il faut obscurcir la relation entre le message original (en clair, c’est-à-dire non chiffré) et le message chiffré. Un exemple très simple est le « chiffre de César », qui consiste à décaler chaque lettre du texte en clair de trois caractères dans l’alphabet :

texte en clair : ASSAUT DANS UNE HEURE
                 ↓↓↓↓↓↓ ↓↓↓↓ ↓↓↓ ↓↓↓↓↓
texte chiffré  : DVVDXW GDQV XQH KHXUH

                 A + 3 lettres = D

Sauf qu’avec le chiffre de César, il est facile d’analyser la fréquence des lettres et de retrouver les mots.

Alors la deuxième grande idée, c’est la diffusion. Cela permet d’éclater le message pour le rendre plus difficile à reconnaître. Un exemple de cette technique, c’est la transposition par colonnes. Ainsi, pour une diffusion en trois points, on répartit le texte sur trois lignes puis on le retranscrit colonne par colonne :

   1  2  3  4  5  6     1   2   3   4   5   6
  ┌─┐┌─┐┌─┐┌─┐┌─┐┌─┐    ↓   ↓   ↓   ↓   ↓   ↓
  │A││S││S││A││U││T│
↓ │D││A││N││S││U││N│ → ADE SAH SNE ASU UUR TNE
  │E││H││E││U││R││E│
  └─┘└─┘└─┘└─┘└─┘└─┘   diffusion en 3 points

Ce que l’on appelle algorithmes de chiffrement, ce sont les différentes techniques utilisées pour transformer le texte original. Quant à la clé de chiffrement, c’est, dans le cas du chiffre de César par exemple, le nombre de caractères de décalage (3, en l’occurrence) ou, dans la technique de diffusion, le nombre de lignes des colonnes. La valeur de cette clé est variable : on aurait tout aussi bien pu décider de faire des colonnes de 2 lignes, ou un décalage de 6 caractères.

Ce qui nous amène à la troisième grande idée : le secret réside seulement dans la clé. Après quelques millénaires, on a constaté que c’était une mauvaise idée de partir du principe que personne n’arriverait à comprendre l’algorithme de chiffrement : tôt ou tard, une personne finira bien par le découvrir. Il est en effet bien plus facile de garder secrète une simple clé de chiffrement ou une phrase de passe plutôt que tout un algorithme.

De nos jours, l’algorithme peut donc être détaillé en long, en large et en travers sur Wikipédia, permettant à n’importe qui de vérifier qu’il n’a pas de point faible particulier, c’est-à-dire que la seule solution pour déchiffrer un message chiffré sera de disposer de la clé qui a été employée avec celui-ci.

5.1.2 Vous voulez un dessin ?

Concrètement, pour assurer la confidentialité de nos données, on utilise deux opérations : le chiffrement, afin de protéger les données, puis le déchiffrement, afin de pouvoir les lire. Ces opérations sont assurées par un logiciel, par exemple GnuPG.

5.1.2.1 Première étape : le chiffrement

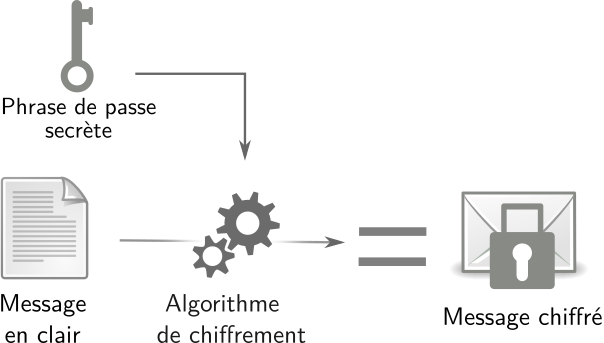
Chiffrement d’un texte en clair

Pour un exemple d’usage pratique, prenons le message suivant¹⁰⁸ :

Les spaghetti sont dans le placard.

Après avoir chiffré ce message en utilisant le logiciel GnuPG avec l’algorithme AES-256 et, comme phrase de passe, « ceci est un secret », on obtiendra par exemple¹⁰⁹ :

Voici donc l’aspect que prend un texte après chiffrement : son contenu est devenu parfaitement incompréhensible. Les données « en clair », lisibles par tout le monde, ont été transformées en un autre format, illisible pour qui ne possède pas la phrase de passe.

5.1.2.2 Deuxième étape : le déchiffrement

Pour le déchiffrement, il nous suffira d’utiliser de nouveau GnuPG, cette fois avec notre texte chiffré. GnuPG nous demandera la phrase de passe ayant servi à chiffrer notre message, et si cette dernière est correcte, on obtiendra enfin l’information qui nous manquait pour préparer le déjeuner.

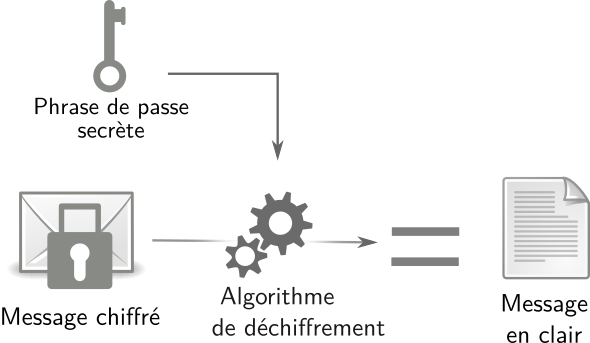
Déchiffrement d’un texte chiffré

5.1.3 Pour un disque dur…

Si l’on souhaite que toutes les données que l’on met sur un support de stockage (disque dur, clé USB, etc.) soient chiffrées, il va falloir que le système d’exploitation se charge de réaliser « à la volée » les opérations de chiffrement et de déchiffrement.

Ainsi, chaque fois que des données devront être lues du disque dur, elles seront déchiffrées au passage afin que les logiciels qui en ont besoin puissent y accéder. À l’inverse, chaque fois qu’un logiciel demandera à écrire des données, elles seront chiffrées avant d’atterrir sur le disque dur.

Pour que ces opérations fonctionnent, il est nécessaire que la clé de chiffrement se trouve en mémoire vive aussi longtemps que le support aura besoin d’être utilisé.

Par ailleurs, la clé de chiffrement ne peut pas être changée. Une fois que cette dernière a servi à chiffrer des données inscrites sur le disque, elle devient indispensable pour pouvoir les relire. Pour pouvoir changer la clé, il faudrait donc relire puis réécrire l’intégralité des données du disque…

Pour éviter cette opération pénible, la plupart des systèmes utilisés pour chiffrer les supports de stockage ont donc une astuce : la clé de chiffrement est en fait un grand nombre aléatoire, qui est lui-même chiffré à l’aide d’une phrase de passe¹¹⁰. Cette version chiffrée de la clé de chiffrement est généralement inscrite sur le support de stockage au début du disque, en « en-tête » des données chiffrées.

Avec ce système, changer la phrase de passe devient simple, vu qu’il suffit de modifier cet en-tête (ce qui est généralement fait automatiquement par ces systèmes de chiffrement).

5.1.4 Résumé et limites

La cryptographie permet donc de bien protéger ses données¹¹¹, en chiffrant tout ou partie de son disque dur comme de tout autre support de stockage (clé USB, CD, etc.), ou de ses communications. De plus, les ordinateurs modernes sont suffisamment puissants pour que nous puissions faire du chiffrement une routine, plutôt que de le réserver à des circonstances spéciales ou à des informations particulièrement sensibles (sinon, cela identifie tout de suite ces dernières comme importantes, alors qu’il vaut mieux les dissoudre dans la masse).

On peut ainsi mettre en place une phrase de passe pour chiffrer tout un disque dur, et/ou donner à certaines personnes une partie chiffrée avec leur propre phrase de passe. Il est également possible de chiffrer individuellement tel ou tel fichier, ou un email, ou une pièce jointe, avec une phrase de passe encore différente.

Cependant, bien qu’il soit un outil puissant et essentiel pour la sécurité des informations, le chiffrement a ses limites, qu’il faut bien avoir à l’esprit lorsqu’on l’utilise.

Comme expliqué auparavant, lorsqu’on accède à des données chiffrées, il est nécessaire de garder deux choses en tête. Premièrement, une fois les données déchiffrées, ces dernières se trouvent au minimum dans la mémoire vive. Deuxièment, tant que des données doivent être chiffrées ou déchiffrées, la mémoire vive contient également la clé de chiffrement.

Toute personne qui dispose de la clé de chiffrement pourra lire tout ce qui a été chiffré avec, et pourra aussi s’en servir pour chiffrer elle-même des données.

Il faut donc faire attention aux éléments suivants :

Le système d’exploitation et les logiciels ont accès aux données et à la clé de chiffrement autant que nous, alors cela dépend de la confiance qu’on met en eux — il s’agit donc de n’installer que des logiciels en lesquels on a confiance.
Quiconque obtient un accès physique à l’ordinateur allumé a, de fait, accès au contenu de la mémoire vive. Lorsqu’un disque chiffré est activé, celle-ci contient, en clair, les données sur lesquelles on a travaillé depuis l’allumage de l’ordinateur (même si elles sont chiffrées sur le disque). Mais elle contient surtout, comme écrit plus haut, la clé de chiffrement, qui peut donc être recopiée. Il vaut donc mieux prendre l’habitude d’éteindre les ordinateurs et de désactiver (démonter, éjecter) les disques chiffrés quand on ne s’en sert pas.
Dans certains cas, il peut être nécessaire de prévoir des solutions matérielles pour pouvoir couper le courant facilement et rapidement¹¹² ; ainsi les disques chiffrés redeviennent inaccessibles sans la phrase de passe — à moins d’effectuer une cold boot attack.
Il reste également possible qu’un enregistreur de frappe ait été installé sur l’ordinateur, et que celui-ci enregistre la phrase de passe.

Aussi, les mathématiques utilisées dans les algorithmes cryptographiques ont parfois des défauts. Et beaucoup plus souvent encore, les logiciels qui les appliquent comportent des faiblesses ou des erreurs. Certains de ces problèmes peuvent, du jour au lendemain, rendre décryptables en quelques clics des données chiffrées avec ce que l’on pensait être la meilleure des protections¹¹³…

Par ailleurs, une certaine limite « légale » vient s’ajouter aux possibles attaques. En France, toute personne qui chiffre ses données est en effet censée donner le code d’accès aux autorités judiciaires lorsqu’elles le demandent, comme l’explique l’article 434-15-2 du Code pénal¹¹⁴ :

Est puni de trois ans d’emprisonnement et de 270 000 € d’amende le fait, pour quiconque ayant connaissance de la convention secrète de déchiffrement d’un moyen de cryptologie susceptible d’avoir été utilisé pour préparer, faciliter ou commettre un crime ou un délit, de refuser de remettre ladite convention aux autorités judiciaires ou de la mettre en œuvre, sur les réquisitions de ces autorités délivrées en application des titres II et III du livre I^er du code de procédure pénale.

Si le refus est opposé alors que la remise ou la mise en œuvre de la convention aurait permis d’éviter la commission d’un crime ou d’un délit ou d’en limiter les effets, la peine est portée à cinq ans d’emprisonnement et à 450 000 € d’amende¹¹⁵.

À noter là-dedans : « susceptible » et « sur les réquisitions », c’est-à-dire que la loi est assez floue pour permettre d’exiger de toute personne détentrice de données chiffrées qu’elle crache le morceau. On peut éventuellement se voir demander la phrase de passe d’un support qui ne serait pas le nôtre… et que nous n’aurions donc pas. Pour autant, la police, même en la personne d’une OPJ¹¹⁶, doit avoir préalablement obtenu l’autorisation d’une magistrate¹¹⁷. De l’autre côté de la Manche, une législation douanière similaire fait planer un risque de prison ferme pour Muhammad Rabbani, directeur de l’organisation CAGE, pour avoir refusé de livrer ses mots de passe à la frontière¹¹⁸.

Contrairement aux attentes de nombreuses personnes¹¹⁹ ¹²⁰, la justice a rejeté l’argument du « droit à ne pas s’auto-incriminer » pour se défendre de ne pas donner sa convention de déchiffrement. Elle a argué que « ces données, déjà fixées sur un support, existent indépendamment de la volonté de la personne suspectée »¹²¹. De plus, la Chambre criminelle de la Cour de cassation a statué « que le code de déverrouillage d’un téléphone mobile peut constituer une clé de déchiffrement, si ce téléphone est équipé d’un moyen de cryptologie »¹²².

Certaines techniques permettent aussi de combiner chiffrement et stéganographie afin de rendre indétectable la présence de données chiffrées : on parle alors de « chiffrement répudiable », de « déni plausible »¹²³, ou de « deniable encryption » en anglais. Certains logiciels comme VeraCrypt¹²⁴ proposent cette fonctionnalité, qui permettrait en théorie de nier à l’autorité judiciaire l’existence de données chiffrées, et donc d’éviter de se retrouver contrainte à en révéler la phrase de passe sous le coup de l’article 434-15-2. Néanmoins, la jurisprudence à ce sujet est pour l’instant inexistante, et l’utilisation d’un chiffrement répudiable n’exclut pas que la justice parvienne par d’autres moyens à démontrer l’existence de données chiffrées. La prudence reste donc de mise.

Depuis 2014¹²⁵, les flics ont aussi le droit de réquisitionner n’importe qui susceptible « d’avoir connaissance des mesures appliquées pour protéger les données » et « de leur remettre les informations permettant d’accéder aux données »¹²⁶.

Néanmoins, des personnes refusent de donner leur convention de chiffrement et le revendiquent au nom du droit à garder le silence et à ne pas s’auto-incriminer¹²⁷, au même titre que d’autres refusent de donner leur ADN, ce qui est là aussi — dans une moindre mesure — pénalement répréhensible.

5.2 S’assurer de l’intégrité de données

Nous avons vu quelques pistes pour assurer la confidentialité de nos données. Toutefois, il peut être aussi important de pouvoir s’assurer de leur intégrité, c’est-à-dire de vérifier qu’elles n’ont pas subi de modifications en cours de route (par accident ou par malveillance, afin d’y introduire des mouchards, par exemple). On peut également vouloir s’assurer de la provenance de nos données, c’est-à-dire en assurer l’authenticité.

5.2.1 La puissance du hachoir

L’essentiel des techniques pour assurer l’intégrité ou l’authenticité reposent sur des outils mathématiques que la cryptographie a baptisés « fonctions de hachage ».

Ces dernières fonctionnent comme des hachoirs, capables de réduire n’importe quoi en tout petits morceaux. Et si notre hachoir fonctionne suffisamment bien pour pouvoir être utilisé en cryptographie, on sait que :

avec les petits morceaux, impossible de reconstituer l’objet original sans essayer tous les objets de la Terre ;
le même objet, une fois passé au hachoir, donnera toujours les mêmes petits morceaux ;
la probabilité que deux objets différents donnent exactement les mêmes petits morceaux est astronomiquement faible.

Lorsque ces propriétés sont réunies, il nous suffit alors de comparer les petits morceaux issus de deux objets pour savoir s’ils étaient identiques.

Les petits morceaux qui sortent de notre hachoir s’appellent plus couramment une somme de contrôle ou une empreinte. Elle est généralement écrite sous une forme qui ressemble à :

f9f5a68a721e3d10baca4d9751bb27f0ac35c7ba

Notre hachoir fonctionne avec des données de n’importe quelle taille et de n’importe quelle forme : on peut tout aussi bien réduire en petits morceaux — c’est-à-dire calculer leurs empreintes — une image, un CD, un logiciel, etc. Ainsi, par exemple, plutôt que de comparer directement le contenu de deux DVD octet par octet, ce qui risque d’être long et fastidieux, on pourra se contenter de comparer leurs empreintes pour déterminer s’ils sont identiques.

Notre hachoir n’est pas magique pour autant. On imagine tout de même bien qu’en réduisant n’importe quoi en petits cubes de taille identique, on peut se retrouver avec les mêmes petits cubes issus de deux objets différents. Cela s’appelle une collision. La probabilité que de tels carambolages mathématiques se produisent par hasard est heureusement astronomiquement faible, sauf lorsqu’il existe des algorithmes pour les provoquer… ce qui est déjà arrivé pour plusieurs fonctions de hachage après quelques années de recherche, comme pour la fonction SHA-1¹²⁸, par exemple. Dans ce cas, la troisième propriété du hachoir n’est plus respectée, et il faut donc cesser de l’utiliser.

5.2.2 Vérifier l’intégrité d’un logiciel

Prenons un exemple : Ana a écrit un programme et le distribue sur des CD, que l’on peut trouver dans des clubs d’utilisatrices de GNU/Linux. Bea a envie d’utiliser le programme d’Ana, mais se dit qu’il aurait été très facile pour une administration mal intentionnée de remplacer un des CD d’Ana par un logiciel malveillant.

Elle ne peut pas aller chercher un CD directement chez Ana, qui habite dans une autre ville. Par contre, elle a rencontré Ana il y a quelque temps, et connaît sa voix. Elle lui téléphone donc, et Ana lui donne la somme de contrôle du contenu du CD, qu’elle a calculée avec une fonction de hachage sûre :

CD d’Ana   →  94d93910609f65475a189d178ca6a45f
              22b50c95416affb1d8feb125dc3069d0

Bea peut ensuite la comparer avec celle qu’elle génère à partir du CD qu’elle s’est procuré, en utilisant la même fonction de hachage :

CD de Bea  →  94d93910609f65475a189d178ca6a45f
              22b50c95416affb1d8feb125dc3069d0

Comme les sommes de contrôle sont identiques, Bea est contente, elle est sûre de bien utiliser le même CD que celui fourni par Ana.

Calculer ces sommes de contrôle ne prend pas beaucoup plus de temps que la lecture complète du CD… soit quelques minutes tout au plus.

Maintenant, mettons-nous dans la peau de Carole, qui a été payée pour prendre le contrôle de l’ordinateur de Bea à son insu. Pour cela, elle veut créer un CD qui ressemble à celui d’Ana, mais qui contient un logiciel malveillant.

Carole commence donc par se procurer le CD original d’Ana. Ensuite, elle modifie ce CD pour y introduire le logiciel malveillant. Cette première version ressemble de très près à l’original. Cela pourrait duper plus d’une personne qui ne ferait pas attention, mais elle sait que Bea vérifiera la somme de contrôle du CD avant d’installer le programme qu’il contient.

Comme Ana utilise une fonction de hachage qui n’a pas de défauts connus, il ne reste à Carole qu’à essayer un très grand nombre de variations des données de son CD, cela dans l’espoir d’obtenir une collision, c’est-à-dire la même somme de contrôle que celle d’Ana.

Malheureusement pour elle, et heureusement pour Bea, même avec de très nombreux ordinateurs puissants et même en y passant un temps extrêmement long, les chances de réussite de Carole resteraient astronomiquement faibles¹²⁹.

Il suffit donc de se procurer une empreinte, ou somme de contrôle, par des intermédiaires de confiance pour vérifier l’intégrité de données. Tout l’enjeu est ensuite de se procurer ces empreintes par un moyen de confiance, c’est-à-dire de pouvoir vérifier leur authenticité…

5.2.3 Vérifier un mot de passe

Un autre exemple d’utilisation des fonctions de hachage concerne la vérification de l’authenticité d’une demande d’accès.

Si l’accès à un ordinateur est protégé par un mot de passe, comme par exemple l’ouverture d’une session sous GNU/Linux¹³⁰, il faut que l’ordinateur puisse vérifier que le mot de passe que l’on entre est le bon. Cependant, les mots de passe ne sont pas enregistrés en clair sur l’ordinateur, sinon il serait trop facile de les obtenir.

Mais alors comment l’ordinateur s’assure-t-il que le mot de passe tapé au clavier est exact ?

Lorsque l’on choisit un mot de passe pour son ordinateur, le système enregistre, grâce à une fonction de hachage, une empreinte du mot de passe. Pour vérifier l’accès, il « hache » de la même manière le mot de passe que l’on a saisi. Et si les empreintes sont les mêmes, il considère que ce mot de passe était le bon.

Il est donc possible de vérifier que le mot de passe correspond, sans garder le mot de passe lui-même !

5.3 Symétrique, asymétrique ?

Les techniques de chiffrement mentionnées jusqu’ici reposent sur une seule clé secrète, qui permet à la fois d’effectuer le chiffrement et le déchiffrement. On parle dans ce cas de cryptographie symétrique.

Ceci en opposition avec la cryptographie asymétrique, qui, dans le contexte du chiffrement, n’utilise pas la même clé pour chiffrer et pour déchiffrer un message. Aussi appelée « cryptographie à clé publique », elle est surtout utilisée pour la communication « en ligne » ; on en parlera donc en détail dans le second tome.

Une des propriétés les plus intéressantes de la cryptographie asymétrique, que l’on peut évoquer brièvement, est la possibilité de réaliser des signatures numériques. Comme son équivalent papier, une signature numérique permet d’apposer une marque de reconnaissance sur des données.

Ces signatures numériques qui utilisent la cryptographie asymétrique constituent la façon la plus simple de vérifier la provenance d’un logiciel. On sera donc amenées à s’en servir plus loin…

Pour un bon aperçu des différentes méthodes — qu’on appelle des « attaques » — couramment utilisées en cryptanalyse, on peut se référer à la page Wikipédia, 2020, Cryptanalyse.↩︎
Le passage qui suit est une adaptation très partielle de la bande dessinée de Jeff Moser sur l’algorithme AES (en anglais).↩︎
Ce message est d’une très haute importance stratégique pour des personnes qu’on inviterait chez soi. Il est donc crucial de le chiffrer. Blague à part, si l’on ne chiffre que des messages « sensibles », tous les messages chiffrés que l’on envoie sont alors suspects ; d’où l’importance de chiffrer aussi des messages anodins.↩︎
Même si l’on chiffre le même message avec la même phrase de passe, le résultat est différent à chaque fois que l’on répète l’opération : afin d’empêcher quiconque de comparer des messages chiffrés (sans en connaître la phrase de passe) pour savoir s’ils correspondent ou non à un même message en clair, des données aléatoires sont introduites afin de rendre chaque message chiffré unique et distinct des autres.↩︎
Le système LUKS, utilisé sous GNU/Linux, permet même d’utiliser plusieurs versions chiffrées de la clé de chiffrement. Chacune de ces versions peut être chiffrée avec une phrase de passe différente, ce qui permet à plusieurs personnes d’accéder aux mêmes données sans pour autant avoir à retenir le même secret.↩︎
Un article de Rue89 sur les révélations de Snowden quant à l’impuissance de la NSA face au chiffrement : Marie Gutbub, 2014, Crimes de guerre et décryptage de données : nouvelles révélations de Snowden.↩︎
Pour cette raison, il peut être recommandé de ne pas laisser la batterie branchée dans un ordinateur portable quand elle n’est pas utilisée. Il suffit alors d’enlever le câble secteur pour l’éteindre.↩︎
Le blog de Zythom, 2015, Le disque dur chiffré.↩︎
Le terme légal est « cryptologie ». Une recherche sur ce mot sur Légifrance donnera une liste exhaustive des textes de loi concernant ce domaine.↩︎
Légifrance, 2016, Code pénal, article 434-15-2.↩︎
Officière de police judiciaire.↩︎
Les Numériques, 2020, Refuser le déverrouillage de son smartphone à la police, une infraction dans certains cas.↩︎
Birkbeck Law Review, 2018, In Conversation with Muhammad Rabbani, CAGE (en anglais).↩︎
Maître Éolas, 2014, Allô oui j’écoute.↩︎
La Quadrature du Net, 2018, Le Conseil constitutionnel restreint le droit au chiffrement.↩︎
Conseil constitutionnel, 2018, Décision n° 2018-696 QPC du 30 mars 2018.↩︎
Légifrance, 2021, Cour de cassation, criminelle, Chambre criminelle, 3 mars 2021, 19-86.757, Inédit.↩︎
Wikipédia, 2020, Déni plausible (cryptologie).↩︎
Site officiel de VeraCrypt (en anglais).↩︎
Légifrance, 2014, Loi n° 2014-1353 du 13 novembre 2014 renforçant les dispositions relatives à la lutte contre le terrorisme.↩︎
Légifrance, Code de procédure pénale, article 57-1.↩︎
Le Parisien, 2018, Un gardé à vue peut garder le silence mais doit donner les codes de son smartphone.↩︎
Marc Stevens et al., 2017, Announcing the first SHA-1 collision, Google Security Blog (en anglais).↩︎
Pour donner un ordre de grandeur de la chose, avec une fonction de hachage parmi celles actuellement considérées comme sûres (SHA-256, par exemple), même si Ana disposait d’un milliard de milliards d’ordinateurs, chacun capable de calculer dix milliards de sommes de contrôle par seconde, et qu’elle les faisait calculer pendant une durée équivalente à l’âge actuel de l’univers (quinze milliards d’années), elle serait encore très loin d’avoir une chance raisonnable de trouver une collision !

Par contre, cela ne tient pas compte d’éventuelles avancées futures en cryptanalyse qui pourraient découvrir des faiblesses dans la fonction de hachage utilisée et proposer des algorithmes plus efficaces pour permettre à Carole de réaliser son attaque dans un temps raisonnable.↩︎
Rappelons-nous que ces mots de passe ne servent pas à protéger les données !↩︎